The activation function of a node defines the output of that node given an input or set of inputs in the neural network. The activation function allows the neural network to learn a non-linear pattern between inputs and target output variable.
A neural network without activation function is just like a linear regression model which is not able to learn the complex non-linear pattern. Hence, the activation function is a key part of the neural network. The following figure shows the linear and non-linear patterns.
There is mainly three activation function used in the neural network. That are listed below:
- Sigmoid
- Tanh – Hyperbolic tangent
- ReLU – Rectified linear unit
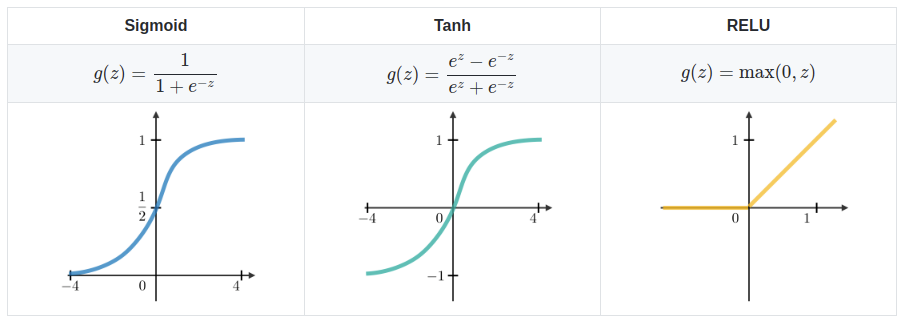
Sigmoid Activation Function
A sigmoid activation function is a mathematical function having a characteristic “S”-shaped curve or sigmoid curve. The sigmoid function takes a real-value as input and generates output value between 0 and 1. It is a non-linear function by nature.
The mathematical equation of the Sigmoid function is :
There is some problem exist with Sigmoid function.
- “vanishing gradients” problem occur
- Slow convergence
- Sigmoids saturate and kill gradients.
- Its output isn’t zero centred. It makes the gradient updates go too far in different directions. 0 < output < 1, and it makes optimization harder.
Note: Sigmoid activation function generally used for the output layer in binary classification problem.
. . .
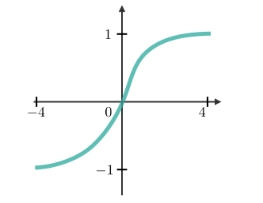
Tanh Activation Function
The Tanh function stands for Hyperbolic tangent. The Tanh function looks similar to Sigmoid function the difference is that Tanh function is zero-centred. Therefore, in practice, the Tanh non-linearity is always preferred to the sigmoid nonlinearity. The range of output value is between -1 to 1. Tanh also has a vanishing gradient problem.
The mathematical equation of the Tanh function is :
. . .
ReLU Activation Function
The ReLU function stands for Rectified Linear Units. It has become most famous in the past few years. The mathematical formula of ReLU activation function is quite simple: max(0, Z). ReLu is less computationally expensive than Tanh and Sigmoid because it involves simpler mathematical operations.
ReLU avoids and rectifies the vanishing gradient problem. The graphical representation of the ReLU function is :
. . .
Summary
