Gradient Descent in Neural Network

The main goal of deep learning algorithms is to minimize the difference between the predicted target value and the actual target value. This is also called Loss function or Cost function.

We can minimize the loss function by finding the optimized value for weight and bias parameters. An algorithm which optimize the loss function is called an optimization algorithm. There are various optimization algorithm exists which are listed below:

• Gradient Descent
• Stochastic Gradient Descent (SGD)
• RMSprop
• Adagrad
• Adadelta
• Adam
• Adamax
• Nadam

This tutorial has explained the Gradient Descent optimization algorithm and also explained its variant algorithms.

Gradient Descent

Gradient Descent is the most famous optimization algorithm in the neural network. We update the weight and bias parameters iteratively in the negative gradient direction to minimize the loss function.

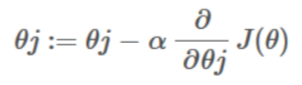
Here,

• α is a learning rate.
• J(θ) is a loss function
• θj is the weight or bias parameter, which we need to update.

There are three main types of Gradient Descent.

• Batch Gradient Descent
• Stochastic Gradient Descent (SGD)
• Mini-batch Gradient Descent

.     .     .

Batch Gradient Descent

It is a variant of the gradient descent algorithm. The Batch Gradient Descent algorithm considers or analysed the entire training data while updating the weight and bias parameters for each iteration. In Batch Gradient Descent, we need to sum up all over the training example on each iteration.

For example, consider the number of training example m = 10 million. The Gradient computation of all over the 10 million training data is computationally very expensive.

.     .     .

Stochastic Gradient Descent (SGD)

Stochastic Gradient Descent is the variant of the Gradient Descent optimization algorithm. The Batch Gradient Descent algorithm considers or analysed the entire training dataset while updating the weight and bias parameters for each iteration. One of the drawbacks of the Gradient Descent method is that if the number of training example is large, then computation complexity will be increased.

To overcome this problem Stochastic Gradient Descent is used. The SGD optimizer considers a single training example to update the parameters for each iteration.

The process of SGD is:

1. Randomly shuffle the training examples.
2. A loop through each training example iteratively.
   1. • Make a prediction of a training example
      • Find the loss
      • Update the weight & bias parameter by finding the gradient of the loss function

Due to frequent updations of weight parameters, there is high fluctuation in the direction of convergence to global minima. In fact, SGD doesn’t actually converge in the same sense as Gradient Descent.

.     .     .

Mini-batch Gradient Descent

Mini-batch Gradient Descent is the variant of the Gradient Descent optimization algorithm. The idea of Mini-batch Gradient Descent is between Batch Gradient Descent and Stochastic Gradient Descent. Mini-batch Gradient Descent split the training example into small batches that are used to calculate model error and update model parameters.

The process of Mini-batch Gradient Descent is:

1. Define the batch size that is the number of training sample consider in a batch.
2. A loop through each batch iteratively.
   1. • Make a prediction of a training example
      • Find the error
      • Update the weight & bias parameter by finding the gradient of the loss function

.     .     .