Linear Regression

Linear Regression is one of the famous algorithm in Machine Learning. Linear Regression model learns to understand the relationship between input variables and the output variable. The representation of Linear Regression is quite simple such, both input variables and output variable are numeric.

The linear regression uses a traditional slope-intercept equation where one scalar factor multiplies to each input variable called coefficient. And one additional coefficient is also added to the equation is called intercept or bias coefficient. There are mainly two types of Linear Regression:

Simple Regression

Simple Regression has a single input variable and a single output variable. For example, the equation of simple linear is like:

y = m*x + b

Here, x is an input variable and y is the output variable also our prediction.

Multivariable Regression

When we have more than a single input variable is called Multivariable Regression. A more complex Multivariable Regression equation looks like:

f(x,y,z) = w1x + w2y + w3z

Where, x,y,z represent the input variable and w₁, w₂, w₃ represent the coefficient.

.     .     .

Example of Simple Regression

Let’s consider a dataset, which has a single called feature house area in square feet and need to predict the sale price of it.

	Area(Sq.ft)	Sale Price($)
1	500	100000
2	600	120000
3	800	150000
4	200	70000
5	350	78000
6	455	90000
7	560	110000

The simple linear regression equation will look like:

Sale Price = w1 * Area + b0

Here,

W₁: The coefficient or weight for the Area independent variable.

Area: It is an input variable feature.

b₀: The intercept where the line intercepts the y-axis. It is also known as bias.

Machine Learning algorithm will try to learn the correct values for weight and bias and approximate the line of best fit.

.     .     .

Cost function

The cost function finds the best optimize value for weight coefficients, which helps us to find the best fit line for data points. The cost function is the error rate between the observation’s target actual value and the predicted target value. The difference between the actual target value and the predicted target value is called error.

Let’s consider mean squared error(MSE) as a cost function. The MSE measured the averaged difference between the actual target values and predicted target values. The main goal is to minimize the error in order to improve the accuracy of the model.

Here, n is the number of observation.

.     .     .

Gradient descent

Gradient descent is a method of updating the weight coefficient iteratively in order to minimize the MSE by calculating the gradient of the cost function. Initially, random values are assigned to each coefficient.

Pred_y = mx+ b
Cost function  = (y - pred_y)2

Cost function :  f(m , b) = (y - (mx+b))2

df/dm = -2x (y - (mx + b))
df/db = -2 (y - (mx+b))

.     .     .

Learning Rate

The learning rate is the hyperparameter that controls the trained model on each iteration. It is the step size or scale factor which is considered while updating the weight and bias coefficient. Choosing an appropriate learning rate is also a challenging task as a too-small value may result in a long training process and large learning rate value has risk to overshoot the optimal point.

.     .     .

Model training with Linear Regression

Model training is the iterative procedure to improve the prediction by looping through the dataset multiple times. On each iteration, the weight and bias coefficient is updated using gradient descent. Model training is terminate when we get minimal error.

In [1]:
import numpy as np
import matplotlib.pyplot as plt

# generate random data-set
np.random.seed(0)
x = np.random.rand(100, 1)
y = 2 + 3 * x + np.random.rand(100, 1)

# plot the variable
plt.scatter(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
Out[1]:
In [2]:
def predict_sales(x, weight, bias):
    return weight*x + bias

In [3]:
def cost_function(x, y, weight, bias):
    data_size = len(x)
    total_error = 0.0
    for i in range(data_size):
        total_error += (y[i] - (weight*x[i] + bias))**2
    return total_error / data_size

In [4]:
def update_weights(x, y, weight, bias, learning_rate):
    weight_deriv = 0
    bias_deriv = 0
    data_size = len(x)
    for i in range(data_size):
        # Calculate partial derivatives
        # -2x(y - (mx + b))
        weight_deriv += -2*x[i] * (y[i] - (weight*x[i] + bias))
        # -2(y - (mx + b))
        bias_deriv += -2*(y[i] - (weight*x[i] + bias))
    # We subtract because the derivatives point in direction of steepest ascent
    weight -= (weight_deriv / data_size) * learning_rate
    bias -= (bias_deriv / data_size) * learning_rate
return weight, bias

In [5]:
def train(x, y, weight, bias, learning_rate, iters):
    cost_history = []
    for i in range(iters):
        weight,bias = update_weights(x, y, weight, bias, learning_rate)
        #Calculate cost for auditing purposes
        cost = cost_function(x, y, weight, bias)
        cost_history.append(cost)
        # Log Progress
        if i % 10 == 0:
            print ("iter:{}  weight:{}  bias:{}  cost:{}".format(i,weight,bias,cost))
    return weight, bias, cost_history

In [6]:
weight, bias, cost_history = train(x, y, 0 ,0 ,0.1 ,50)
Out[6]:
iter:0     weight:[0.42198865]     bias:[0.78929265]     cost:[9.34952405]
iter:10     weight:[1.74059406]     bias:[2.9879798]     cost:[0.2134892]
iter:20     weight:[1.94959115]     bias:[3.04804582]     cost:[0.15774209]
iter:30     weight:[2.07759377]     bias:[2.99278683]     cost:[0.138376]
iter:40     weight:[2.18626937]     bias:[2.93826919]     cost:[0.12367039]

In [7]:
regression_line = [(weight*e)+bias for e in x]
plt.scatter(x,y)
plt.plot(x, regression_line)
plt.show()
Out[7]:

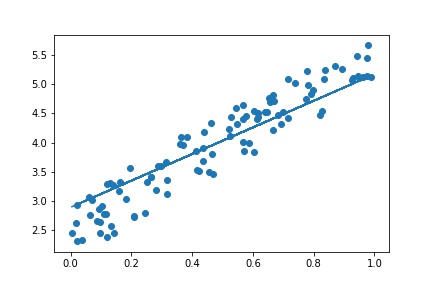
Let’s train linear regression model using Scikit-Learn library.

In [7]:
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(x, y)

In [8]: reg.coef_
Out[8]: [2.93655106]

In [9]: reg.intercept_
Out[9]: [2.55808002]

.     .     .